Problem Link: LeetCode
We are given a matrix in which the rows are sorted, and columns are sorted. WE have to find the kth smallest element in the matrix. There are many approaches. Applying Binary Search is one of them. Its time complexity is bit better than the others. I have tried to explain the binary search approach in this article.
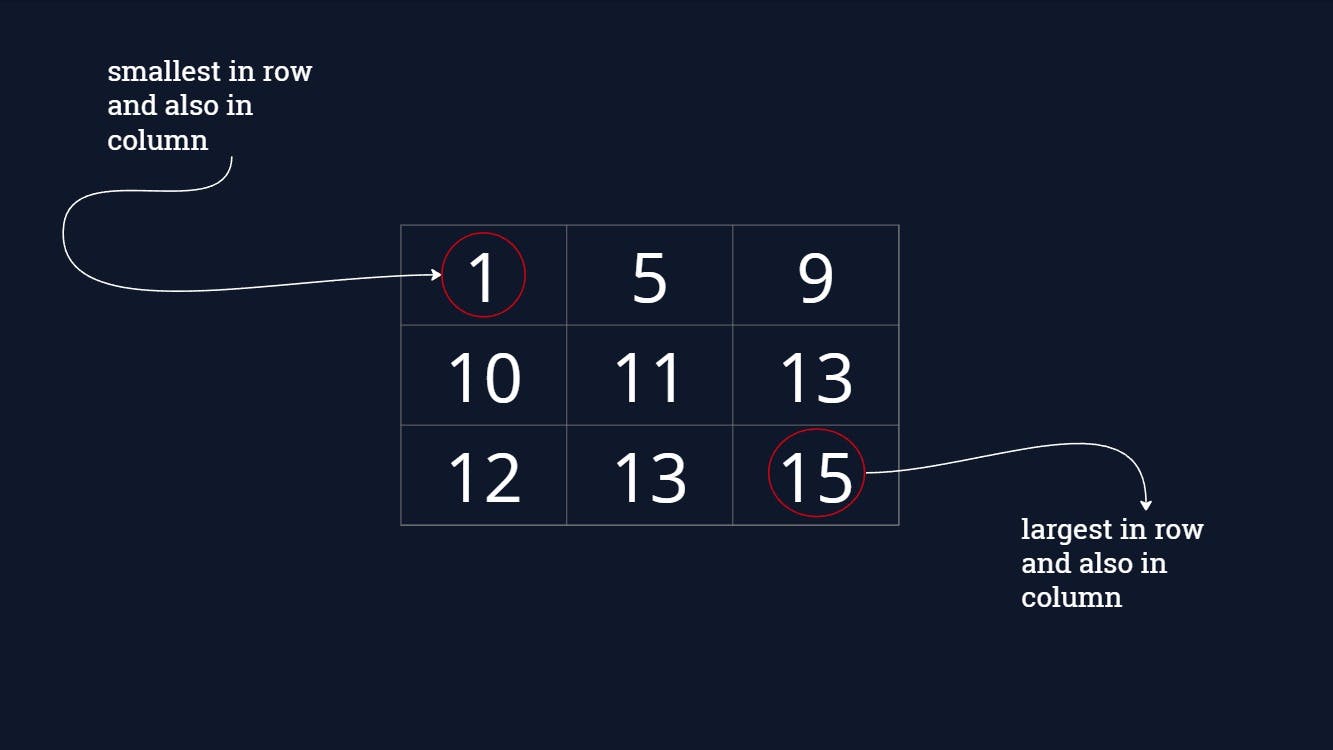
Observing Test Case 1
Suppose we have to find k=8th smallest element from the matrix given.
We have the search range from the (0,0)th element to (n-1,n-1)th element. Because they are sorted in row-wise and also in column-wise.
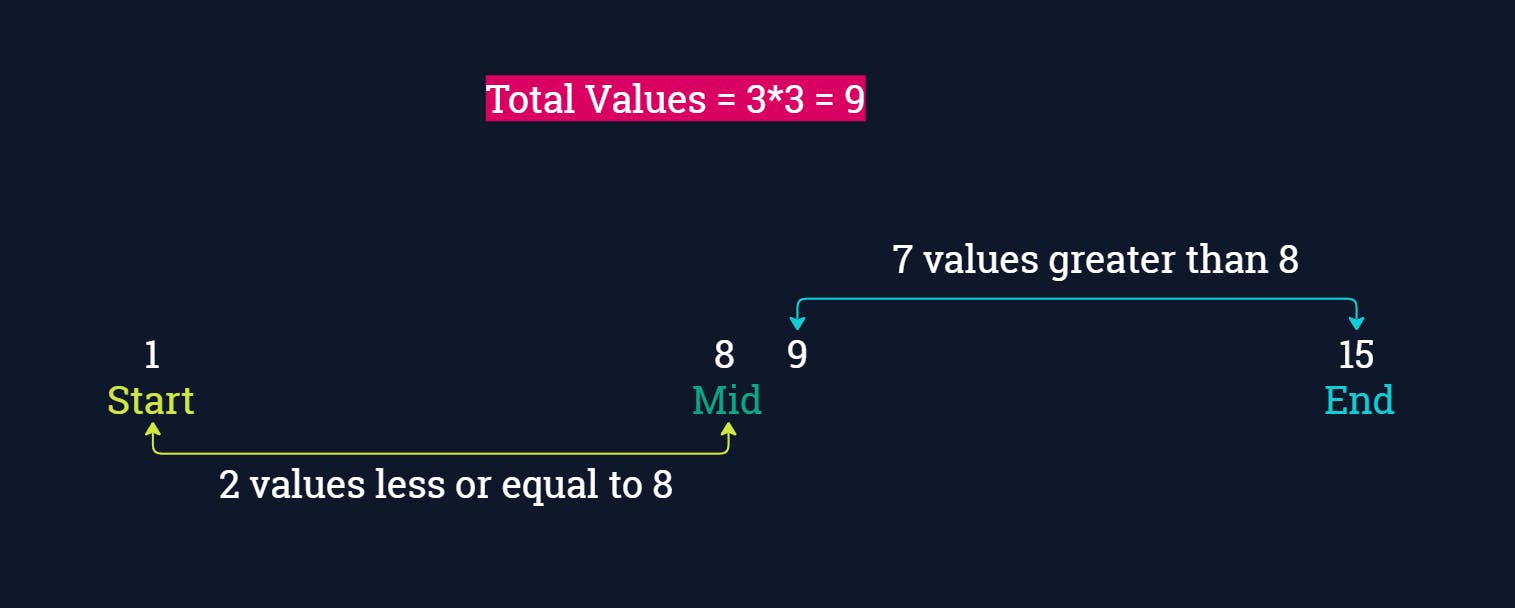
Now we can calculate the mid from the range.

Now it's time to think logically. We have a mid-value which is 8. We can count the numbers of element less or equal to the mid value present in the matrix.

Since, 2 < k(8) If we search in values less than or equal to 8(mid) we won't be able to find 8th one. For 8rd one we have to look into the values greater than 8.
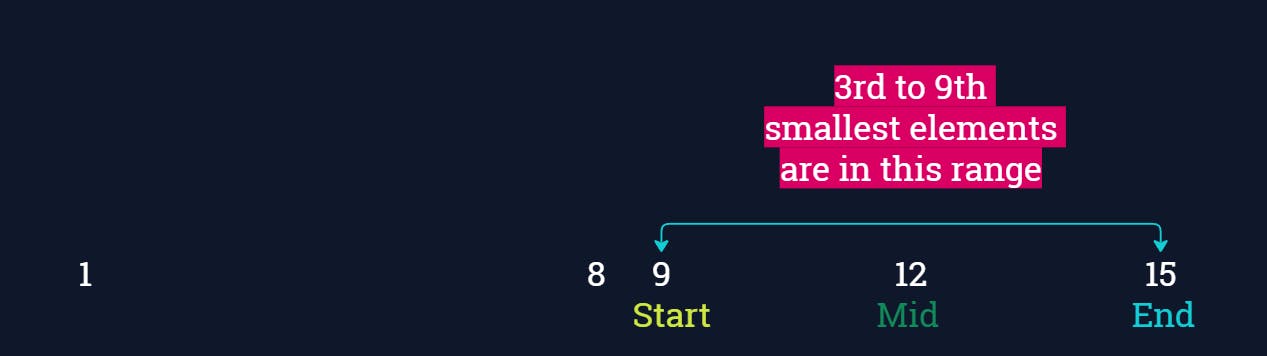
So we move the Start pointer to the mid+1 . Our search space is reduced. The new mid is now (9+15)/2 = 12
let's count how many numbers in the matrix are less than or equal to mid(12) which is 6.

still its less than k(8) so we have to search the right side of mid(12)

Now the count is equal to 8 means there are 8 elements less or equal to the current mid (14).

14 is the answer? No, not really. 14 is not present in the given matrix. We have to find an element that is present in the matrix. The 8th element is 14 or less than 14 we can be sure about that. Can we do end = mid -1 ?? No, because 14 can also be the answer still we don't know. So, the search space should be reduced to mid only. next search space should be 13 to 14.

what is the count for elements less or equal to 13? its still 8.

Since count(8) = k(8) we again reduce the search space to from end to mid only.
end = mid

We an build a table for the better understanding.
| Start | End | Mid | Values less or equal to Mid (count) |
| 1 | 15 | 8 | 2 |
| 9 | 15 | 12 | 6 |
| 13 | 15 | 14 | 8 |
| 13 | 14 | 13 | 8 |
| 13 | 13 | - | - |
Observing Test Case 2
I know we haven't covered the case for moving our start. For that let's see another example.

Here we have to find the k=3rd element in the matrix. Values less or equal to 30 are { 10, 15, 20, 24, 25, 29, 30}. Number of values = 7 which is greater than k(3)
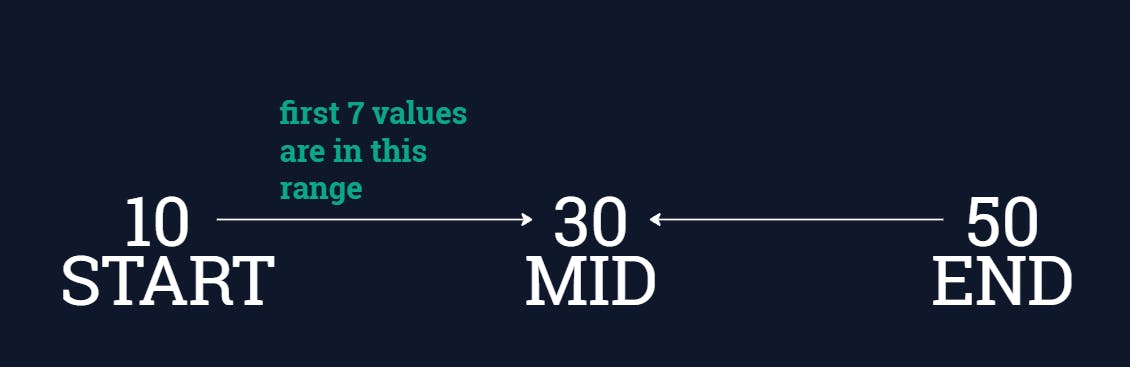
so we have to reduce the search space and bring the end to the mid. why not mid-1? we'll see that later.
Let's follow the table for the rest.
| Start | End | Mid | Values less or equal to mid (Count) |
| 10 | 50 | 30 | 7 |
| 10 | 30 | 20 | 3 ( its the answer but we can't stop we have to continue till start becomes equal to end.) |
| 10 | 20 | 15 | 2 |
| 16 | 20 | 18 | 2 |
| 19 | 20 | 19 | 2 |
| 20 | 20 | - | - |
Let's write the code for up to this.
import java.util.Scanner;
public class Kth_smallest_element {
// we'll improve this method getNumbersLessOrEqual() later.
public static int getNumbersLessOrEqual(int[][] matrix, int mid) {
int n = matrix[0].length;
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] <= mid) {
count++;
}
}
}
return count;
}
public static int kthSmallest(int[][] matrix, int k) {
int n = matrix[0].length;
int start = matrix[0][0];
int end = matrix[n - 1][n - 1];
while (start < end) {
int mid = start + (end - start) / 2;
int count = getNumbersLessOrEqual(matrix, mid);
if (count < k) {
start = mid + 1;
} else {
end = mid;
}
}
return start;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int t = in.nextInt();
while (t-- > 0) {
int n = in.nextInt();
int k = in.nextInt();
int[][] mat = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
mat[i][j] = in.nextInt();
}
}
System.out.println(kthSmallest(mat, k));
}
}
}
Now, see we would do end = mid -1 for having less count than k in that case what would happen?
Let's see another test case for this.
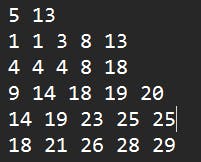
we can directly write down the table for this for k = 13
| start | end | mid | values less or equal to mid |
| 1 | 29 | 15 | 12 |
| 16 | 29 | 22 | 19 |
| 16 | 21 (mid-1) | 18 | 15 |
| 16 | 17 (mid-1) | 16 | 12 |
| 17 | 17 | - | - |
But 17 is not in the matrix. If we take end = mid-1 then we are not being in the search space we need to be. So, it should be end = mid.
Improving the counting method
We were linearly searching through every row and column. Since the rows are sorted respectively, we can apply binary search in each of them. If we can find the index of the largest element greater than the target we found the count of the numbers less or equal to a certain value(mid).
import java.util.Scanner;
public class Kth_smallest_element {
public static int upperBound(int[] arr, int t) {
int start = 0;
int end = arr.length - 1;
while (start <= end) {
int mid = start + (end - start) / 2;
if (t >= arr[mid]) {
start = mid + 1;
} else {
end = mid - 1;
}
}
return start;
}
public static int getNumbersLessOrEqual(int[][] matrix, int mid) {
int n = matrix[0].length;
int count = 0;
for (int i = 0; i < n; i++) {
count += (upperBound(matrix[i], mid));
}
return count;
}
public static int kthSmallest(int[][] matrix, int k) {
int n = matrix[0].length;
int start = matrix[0][0];
int end = matrix[n - 1][n - 1];
while (start < end) {
int mid = start + (end - start) / 2;
int count = getNumbersLessOrEqual(matrix, mid);
if (count < k) {
start = mid + 1;
} else {
end = mid;
}
}
return start;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int t = in.nextInt();
while (t-- > 0) {
int n = in.nextInt();
int k = in.nextInt();
int[][] mat = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
mat[i][j] = in.nextInt();
}
}
System.out.println(kthSmallest(mat, k));
}
}
}
